Write a program that lets the user enter 20 numerical values into an array and then sorts them in ascending order using the bubble sort algorithm.
Solution
The bubble sort algorithm is probably one of the most inefficient sorting algorithms but it is widely used for teaching purposes. The main idea (when asked to sort an array in ascending order) is to repeatedly move the smallest elements of the array to the positions of lowest index. This works as follows: the algorithm iterates through the elements of the array, compares each pair of adjacent elements, and then swaps their contents (if they are in the wrong order). This process is repeated many times until the array is sorted.
For example, let’s try to sort the following array in ascending order.
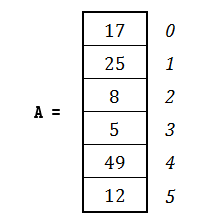
The lowest value is the value 5. According to the bubble sort algorithm, this value should gradually “bubble” or “rise” to position 0, like bubbles rising in a glass of cola. When the value 5 has been moved into position 0, the next smallest value is the value 8. Now, the value 8 should “bubble” to position 1. Next is the value 12, which should “bubble” to position 2, and so on. This process repeats until all elements are placed in proper position.
But how can this “bubbling” be done using an algorithm? Let’s see the whole process in more detail. For the previous array A of six elements, five passes must be performed.
First Pass
1st Compare
Initially, elements at index positions 4 and 5 are compared. Since the value 12 is less than the value 49, these two elements swap their content.
2nd Compare
Elements at index positions 3 and 4 are compared. Since the value 12 is not less than the value 5, no swapping is done.
3rd Compare
Elements at index positions 2 and 3 are compared. Since the value 5 is less than the value 8, these two elements swap their content.
4th Compare
Elements at index positions 1 and 2 are compared. Since the value 5 is less than the value 25, these two elements swap their content.
5th Compare
Elements at index positions 0 and 1 are compared. Since the value 5 is less than the value 17, these two elements swap their content.
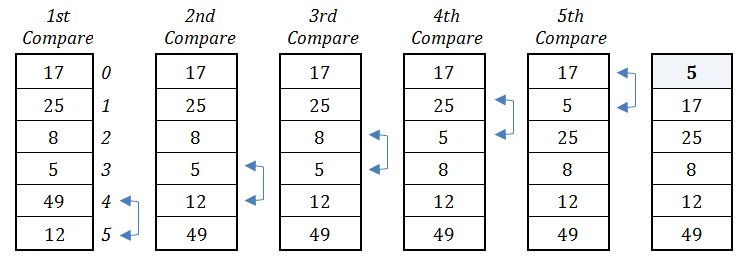
The first pass has been completed but, as you can see, the array has not been sorted yet. The only value that has actually been placed in proper position is the value 5. However, since more passes will follow, there is no need for the value 5 to take part in the subsequent compares. In the pass that follows, one less compare will be performed—that is, four compares.
Second Pass
1st Compare
Elements at index positions 4 and 5 are compared. Since the value 49 is not less than the value 12, no swapping is done.
2nd Compare
Elements at index positions 3 and 4 are compared. Since the value 12 is not less than the value 8, no swapping is done.
3rd Compare
Elements at index positions 2 and 3 are compared. Since the value 8 is less than the value 25, these two elements swap their content.
4th Compare
Elements at index positions 1 and 2 are compared. Since the value 8 is less than the value 17, these two elements swap their content.
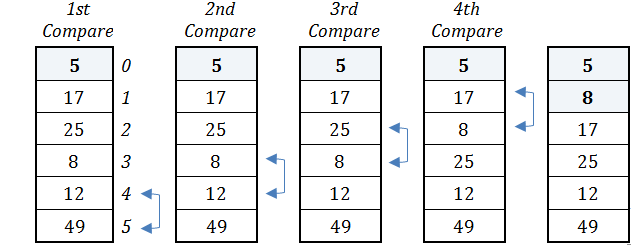
The second pass has been completed and the value of 8 has been placed in proper position. However, since more passes will follow, there is no need for the value 8 (nor 5, of course) to take part in the subsequent compares. In the pass that follows, one less compare will be performed—that is, three compares.
Third Pass
1st Compare
Elements at index positions 4 and 5 are compared. Since the value 49 is not less than the value 12, no swapping is done.
2nd Compare
Elements at index positions 3 and 4 are compared. Since the value 12 is less than the value 25, these two elements swap their content.
3rd Compare
Elements at index positions 2 and 3 are compared. Since the value 12 is less than the value 17, these two elements swap their content.
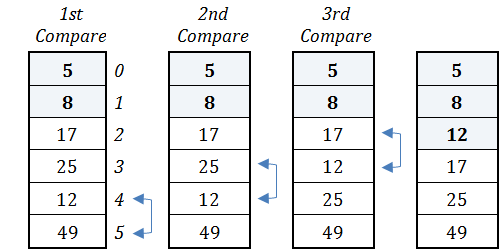
The third pass has been completed and the value of 12 has been placed in proper position. As previously, since more passes will follow there is no need for the value 12 (nor the values 5 and 8, of course) to take part in the subsequent compares. In the pass that follows, one compare less will be performed—that is, two compares.
Fourth Pass
1st Compare
Elements at index positions 4 and 5 are compared. Since the value 49 is not less than the value 25, no swapping is done.
2nd Compare
Elements at index positions 3 and 4 are compared. Since the value 25 is not less than the value 17, no swapping is done.
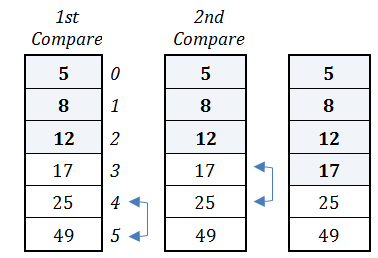
The fourth pass has been completed and the value 17 has been placed in proper position. As previously, since one last pass will follow, there is no need for the value 17 (nor the values 5, 8, and 12, of course) to take part in the subsequent compares. In the last pass that follows, one compare less will be performed—that is one compare.
Fifth pass
1st Compare
Elements at index positions 4 and 5 are compared. Since the value 49 is not less than the value 12, no swapping is done.
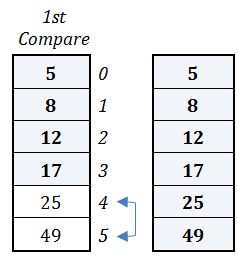
The fifth pass has been completed and the final two values (25 and 49) have been placed in proper position. The bubble sort algorithm has finished and the array is sorted in ascending order!
Now you need a program that can do the whole previous process. Let’s use the “from inner to outer” method. The code fragment that performs the first pass is shown below. Please note that this is the inner (nested) loop control structure.
PHP
Assume variable m contains the value 1.
for ($n = ELEMENTS - 1; $n >= $m; $n--) {
if ($a[$n] < $a[$n - 1]) {
$temp = $a[$n];
$a[$n] = $a[$n - 1];
$a[$n - 1] = $temp;
}
}
Notice: In the first pass, variable
mmust contain the value 1. This assures that at the last iteration, the elements that are compared are those at positions 1 and 0.Notice: The second pass can be performed if you just re-execute the previous code fragment. Variable m, however, needs to contain the value 2. This will ensure that the element at position 0 won’t be compared again. Similarly, for the third pass, the previous code fragment can be re-executed but variable m needs to contain the value 3 for the same reason.
Java
Assume variable m contains the value 1.
for (n = ELEMENTS - 1; n >= m; n--) {
if (a[n] < a[n - 1]) {
temp = a[n];
a[n] = a[n - 1];
a[n - 1] = temp;
}
}
Notice: In the first pass, variable
mmust contain the value 1. This assures that at the last iteration, the elements that are compared are those at positions 1 and 0.Notice: The second pass can be performed if you just re-execute the previous code fragment. Variable
m, however, needs to contain the value 2. This will ensure that the element at position 0 won’t be compared again. Similarly, for the third pass, the previous code fragment can be re-executed but variablemneeds to contain the value 3 for the same reason.
C++
Assume variable m contains the value 1.
for (n = ELEMENTS - 1; n >= m; n--) {
if (a[n] < a[n - 1]) {
temp = a[n];
a[n] = a[n - 1];
a[n - 1] = temp;
}
}
Notice: In the first pass, variable
mmust contain the value 1. This assures that at the last iteration, the elements that are compared are those at positions 1 and 0.Notice: The second pass can be performed if you just re-execute the previous code fragment. Variable
m, however, needs to contain the value 2. This will ensure that the element at position 0 won’t be compared again. Similarly, for the third pass, the previous code fragment can be re-executed but variablemneeds to contain the value 3 for the same reason.
C#
Assume variable m contains the value 1.
for (n = ELEMENTS - 1; n >= m; n--) {
if (a[n] < a[n - 1]) {
temp = a[n];
a[n] = a[n - 1];
a[n - 1] = temp;
}
}
Notice: In the first pass, variable
mmust contain the value 1. This assures that at the last iteration, the elements that are compared are those at positions 1 and 0.Notice: The second pass can be performed if you just re-execute the previous code fragment. Variable
m, however, needs to contain the value 2. This will ensure that the element at position 0 won’t be compared again. Similarly, for the third pass, the previous code fragment can be re-executed but variablemneeds to contain the value 3 for the same reason.
Visual Basic
Assume variable m contains the value 1.
For n = ELEMENTS - 1 To m Step -1
If a(n) < a(n - 1) Then
temp = a(n)
a(n) = a(n - 1)
a(n - 1) = temp
End If
Next
Notice: In the first pass, variable
mmust contain the value 1. This assures that at the last iteration, the elements that are compared are those at positions 1 and 0.Notice: The second pass can be performed if you just re-execute the previous code fragment. Variable
m, however, needs to contain the value 2. This will ensure that the element at position 0 won’t be compared again. Similarly, for the third pass, the previous code fragment can be re-executed but variablemneeds to contain the value 3 for the same reason.
Python
Assume variable m contains the value 0.
for n in range(ELEMENTS - 1, m, -1):
if a[n] < a[n - 1]:
a[n], a[n - 1] = a[n - 1], a[n]
Notice: In the first pass, variable
mmust contain the value 0. This assures that at the last iteration, the elements that are compared are those at positions 1 and 0.Notice: The second pass can be performed if you just re-execute the previous code fragment. Variable m, however, needs to contain the value 1. This will ensure that the element at position 0 won’t be compared again. Similarly, for the third pass, the previous code fragment can be re-executed but variable m needs to contain the value 2 for the same reason
The previous code fragment needs to be executed five times (one for each pass), and each time variable
m must be incremented by 1. The final code fragment that sorts array a using the bubble sort algorithm is as follows.
PHP
for ($m = 1; $m <= ELEMENTS - 1; $m++) {
for ($n = ELEMENTS - 1; $n >= $m; $n--) {
if ($a[$n] < $a[$n - 1]) {
$temp = $a[$n];
$a[$n] = $a[$n - 1];
$a[$n - 1] = $temp;
}
}
}
Java
for (m = 1; m <= ELEMENTS - 1; m++) {
for (n = ELEMENTS - 1; n >= m; n--) {
if (a[n] < a[n - 1]) {
temp = a[n];
a[n] = a[n - 1];
a[n - 1] = temp;
}
}
}
C++
for (m = 1; m <= ELEMENTS - 1; m++) {
for (n = ELEMENTS - 1; n >= m; n--) {
if (a[n] < a[n - 1]) {
temp = a[n];
a[n] = a[n - 1];
a[n - 1] = temp;
}
}
}
C#
for (m = 1; m <= ELEMENTS - 1; m++) {
for (n = ELEMENTS - 1; n >= m; n--) {
if (a[n] < a[n - 1]) {
temp = a[n];
a[n] = a[n - 1];
a[n - 1] = temp;
}
}
}
Visual Basic
For m = 1 To ELEMENTS - 1
For n = ELEMENTS - 1 To m Step -1
If a(n) < a(n - 1) Then
temp = a(n)
a(n) = a(n - 1)
a(n - 1) = temp
End If
Next
Next
Python
for m in range(ELEMENTS - 1):
for n in range(ELEMENTS - 1, m, -1):
if a[n] < a[n - 1]:
a[n], a[n - 1] = a[n - 1], a[n]
The complete program is as follows.
PHP
<?php
define("ELEMENTS", 20);
$a = array();
for ($i = 0; $i <= ELEMENTS - 1; $i++) {
$a[$i] = trim(fgets(STDIN));
}
for ($m = 1; $m <= ELEMENTS - 1; $m++) {
for ($n = ELEMENTS - 1; $n >= $m; $n--) {
if ($a[$n] < $a[$n - 1]) {
$temp = $a[$n];
$a[$n] = $a[$n - 1];
$a[$n - 1] = $temp;
}
}
}
for ($i = 0; $i <= ELEMENTS - 1; $i++) {
echo $a[$i], "\t";
}
?>
Java
static final int ELEMENTS = 20;
public static void main(String[] args) throws java.io.IOException {
java.io.BufferedReader cin = new java.io.
BufferedReader(new java.io.InputStreamReader(System.in));
int i, m, n;
double temp;
double[] a = new double[ELEMENTS];
for (i = 0; i <= ELEMENTS - 1; i++) {
a[i] = Double.parseDouble(cin.readLine());
}
for (m = 1; m <= ELEMENTS - 1; m++) {
for (n = ELEMENTS - 1; n >= m; n--) {
if (a[n] < a[n - 1]) {
temp = a[n];
a[n] = a[n - 1];
a[n - 1] = temp;
}
}
}
for (i = 0; i <= ELEMENTS - 1; i++) {
System.out.print(a[i] + "\t");
}
}
C++
#include <iostream>
using namespace std;
const int ELEMENTS = 20;
int main() {
int i, m, n;
double temp;
double a[ELEMENTS];
for (i = 0; i <= ELEMENTS - 1; i++) {
cin >> a[i];
}
for (m = 1; m <= ELEMENTS - 1; m++) {
for (n = ELEMENTS - 1; n >= m; n--) {
if (a[n] < a[n - 1]) {
temp = a[n];
a[n] = a[n - 1];
a[n - 1] = temp;
}
}
}
for (i = 0; i <= ELEMENTS - 1; i++) {
cout << a[i] << "\t";
}
return 0;
}
C#
const int ELEMENTS = 20;
static void Main() {
int i, m, n;
double temp;
double[] a = new double[ELEMENTS];
for (i = 0; i <= ELEMENTS - 1; i++) {
a[i] = Double.Parse(Console.ReadLine());
}
for (m = 1; m <= ELEMENTS - 1; m++) {
for (n = ELEMENTS - 1; n >= m; n--) {
if (a[n] < a[n - 1]) {
temp = a[n];
a[n] = a[n - 1];
a[n - 1] = temp;
}
}
}
for (i = 0; i <= ELEMENTS - 1; i++) {
Console.Write(a[i] + "\t");
}
Console.ReadKey();
}
Visual Basic
Const ELEMENTS = 20
Sub Main()
Dim i, m, n As Integer
Dim temp As Double
Dim a(ELEMENTS - 1) As Double
For i = 0 To ELEMENTS - 1
a(i) = Console.ReadLine()
Next
For m = 1 To ELEMENTS - 1
For n = ELEMENTS - 1 To m Step -1
If a(n) < a(n - 1) Then
temp = a(n)
a(n) = a(n - 1)
a(n - 1) = temp
End If
Next
Next
For i = 0 To ELEMENTS - 1
Console.Write(a(i) & vbTab)
Next
Console.ReadKey()
End Sub
Python
ELEMENTS = 20
a = [None] * ELEMENTS
for i in range(ELEMENTS):
a[i] = float(input())
for m in range(ELEMENTS - 1):
for n in range(ELEMENTS - 1, m, -1):
if a[n] < a[n - 1]:
a[n], a[n - 1] = a[n - 1], a[n]
for i in range(ELEMENTS):
print(a[i], end = "\t")
Notice: The bubble sort algorithm is very inefficient. The total number of compares that it performs is
, where N is the total number of array elements.
Notice: The total number of swaps depends on the given array. The worst case is when you want to sort in descending order an array that is already sorted in ascending order, or vice versa.